LBM的迁移，实际上就是数组元素的平移。

做迁移的时候，最需要注意的就是数值覆盖。所以用C来实现的时候，替代的顺序和传递的顺序应该是相反的。D2Q9的离散格式如下：

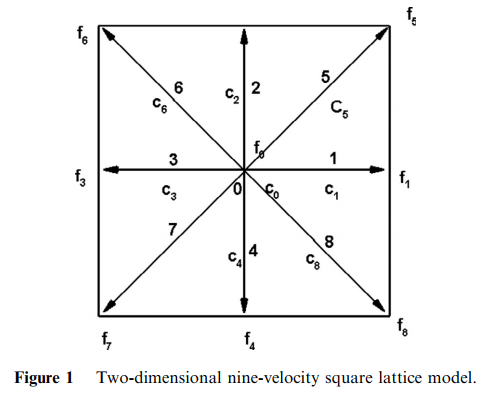
D2Q9
D2Q9

f1(i+1)=f(i)
f3(i)=f3(i+1)
以此类推。

一种C形式的迁移

用for循环语句：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#f1,f3
for j=1:m
    for i=n:-1:2
        f(i,j,1)=f(i-1,j,1);
    end
    for i=1:(n-1)
        f(i,j,3)=f(i+1,j,3);
    end
end
#f2,f5,f6
for j=m:-1:2
    for i=1:n
        f(i,j,2)=f(i,j-1,2);
    end
    for i=n:-1:2
        f(i,j,5)=f(i-1,j-1,5);
    end
    for i=1:(n-1)
        f(i,j,6)=f(i+1,j-1,6);
    end
end
#f4,f7,f8
for j=1:(m-1)
    for i=1:n
        f(i,j,4)=f(i,j+1,4);
    end
    for i=1:(n-1)
        f(i,j,7)=f(i+1,j+1,7);
    end
    for i=n:-1:2
        f(i,j,8)=f(i-1,j+1,8);
    end
end

这种方式的代码可以很方便的改成C语言。

2 数组操作型

在MATLAB里面实现这个还有更简洁的方式：

1
2
3
4
5
6
7
8
f(2:n,:,1)=f(1:n-1,:,1);
f(:,2:m,2)=f(:,1:m-1,2);
f(1:n-1,:,3)=f(2:n,:,3);
f(:,1:m-1,4)=f(:,2:m,4);
f(2:n,2:m,5)=f(1:n-1,1:m-1,5);
f(1:n-1,2:m,6)=f(2:n,1:m-1,6);
f(1:n-1,1:m-1,7)=f(2:n,2:m,7);
f(2:n,1:m-1,8)=f(1:n-1,2:m,8);

这种实现和第一种没有本质区别。只是代码显得更简洁。但是如果向其他离散形式进行拓展，比如像三维D3Q15这种就不适合了，需要手动写很多代码。
所以一个更简单，推广性更好的实现是使用数组平移函数circshift。

3 使用circshift

circshift是一个数组平移函数。

这种方式circshift是一个循环平移函数，这里的循环实际上我们并不需要。

假设a=[1,2,3,4,5]，我们执行b=circshift(a,1)会得到：

circshift
circshift

讲道理，我们不需要把5移动到b(1)，而希望b(1)=a(1)。所以执行完这个以后，需要对边界进行处理。

代码如下：

1
2
3
4
5
6
7
8
9
10
for i=1:9
   b(i)=circshift(f(:,:,i),[cx(i),cy(i),0]);
   #x和y的起始点
   qsdx=1+0.5*(cx(i)^2+cx(i));
   qsdy=1+0.5*(cy(i)^2+cy(i));
   #x和y的终点
   zdx=n+0.5(cx(i)-cx(i)^2));
   zdy=m+0.5(cy(i)-cy(i)^2));
   f(qsdx:zdx,qsdy:zdy)=b(qsdx:zdx,qsdy:zdy);
end

这里构造了起始点和终点函数。想象一下，假设平移向量是（1，-1）。那么我们需要的是在x方向从2到n，在y方向需要的是从1到m-1。
于是构造了起始点和终点的函数分别为：

$$
x_{qsd} = 1 + { {c{x^2} + cx} \over 2}
$$

$$
{x_{zd}} = n + { {cx - c{x^2} } \over 2}
$$

这里给的是x方向的，y方向的构造一模一样，只不过cx改为cy，n改为m而已。把平移函数cx=1，cy=-1代入公式，可以得到起始点和终点为：

$$
\eqalign{
& x = 2:n \cr
& y = 1:m - 1 \cr}
$$
这和我们需要的数据是一模一样的。
这个方法的拓展性比较好，不需要针对不同的离散格子模型全部重写代码。